一些ACM计数问题——球盒模型等

发表于 2024-03-25 Disqus：

一些ACM计数问题——球盒模型等

1. 前置知识1

1.1 组合数

组合数的意义是从个不同的球中取出个球的方案数（）。

它的公式是：.

一般很少用它的递推形式：.

1.2 隔板法

在一系列的球之间选几个缝隙，插入板，就是隔板问题。

例如个球之间插入块板，可以将其分成组球（每组至少有一个球）。

由于个球之间有个缝隙，从中选出个缝隙，所对应的方案数是。

1.3 生成函数

没学过生成函数的推荐 https://www.bilibili.com/video/BV1E24y1171z?vd_source=a18dbba15826659c13a0c2fac0a3673c

笼统来讲，对于一个有限or无限的数列，它对应的生成函数为 .

生成函数主要解决以下问题：

有种不同的物品，其中第种物品可以取出个，问总共取出个物品的方案数。

对于第种物品的生成函数为：.

我们将个生成函数进行相乘，得到的多项式中项所对应的系数就是要求的答案。

具体实现复杂度为，可以使用 FFT 进行进一步优化。（但是我不会FFT

1.4 五边形数

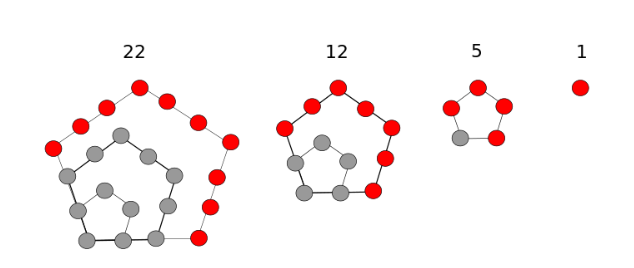
五边形数就是如上图所示的点的个数。第个五边形数相比于第个五边形数，多出了红色的点，它的个数为。因此有 .

可通过差分前缀和求得通项公式：.

如果将的定义域扩展到负数，则有广义五边形数

关于五边形数，有五边形数定理：

欧拉函数

这个定理在后续正文讨论中会使用。

2. 正文1

球盒模型，是指将个球放到个盒中的方案计数问题。但是根据以下三项不同的要求，有8种变形：

球是否相同
盒子是否相同
盒子是否可以为空

接下来让我们一一进行解决。

1. 球相同，盒子不同，盒子不可以为空

等价于将球分为组。根据前置知识的隔板法，相当于在个缝隙中插入个板，对应的方案数为

2. 球相同，盒子不同，盒子可以为空

上个问题对于盒子的要求是：至少有一个球。

而本问题对于盒子的要求是：至少有零个球。

我们可以考虑将总球数增加，然后进行上个问题的求解。

这样所对应的问题是：个相同球与个不同的盒子，每个盒子至少有一个球。

然后我们可以把每个盒子中的每个球都删去一个，这样每个盒子都至少有零个球。此时总球数减少了，为个。

因此问题转化为：个相同球与个不同的盒子，每个盒子至少有零个球。

可以发现和本问题是一模一样的。答案为

3. 球相同，盒子相同，盒子可以为空

可以使用动态规划解决，个人感觉这个dp的转移算是比较难想的啦。

令表示将个球分到个盒子里的方案数。

关于状态转移，可以分为以下两中情况：

1、个盒子内，至少有一个盒子为空。由于盒子相同，所以我们可以将这个盒子去掉，方案数为；

2、个盒子内，每个盒子都至少有一个球。这种情况等价于把所有盒子内部去掉一个球的情况，方案数为。

因此可得转移方程：.

显然复杂度是的。

事实上，这个问题的特殊情况等价于整数划分问题，这里我们讨论一下：

一个整数可以用多少种方式划分为其他整数的和？例如：

5=1+1+1+1+1

5=1+1+1+2

5=1+2+2

5=1+1+3

5=2+3

5=1+4

5=5

这里我们把每个整数都看作一个物品，盒子有个。朴素dp做法复杂度为。

我们这样考虑，一个整数能够表示，其对应的生成函数为：.

我们要求的，是将所有的生成函数进行累乘后得到的多项式中所对应的系数：.

在前置知识中，我们提到欧拉函数

因此，，即 .

将这个庞大的式子转化成多项式，根据多项式乘法，项所对应的系数为：.

这里的要满足 .

然而，除了常数项为，其余带项的系数都应该为。

因此令上式子为，得到 .

可以发现这是一个递推的形式。由于广义五边形数的量级为，因此这里递推一次的复杂度为，总复杂度为 .

4. 球相同，盒子相同，盒子不可以为空

和第一二种情况类似，该问题对盒子的要求是：至少一个球

而上个问题的要求是：至少零个球

因此我们把每个盒子都减去一个球，事实上求的就是上述dp解法的 .

当然，我们可以对这道题单独定义一个dp状态。

然后根据上问题的转移，我们将状态分为“至少有一个盒子只有一个球”和“所有盒子都至少有大于一个球”的情况，得到转移式子：

原题链接：https://www.luogu.com.cn/problem/P1025

到目前为止，我们将所有球相同的情况都逐一进行了解读。事实上，正是球相同的这个性质，让我们可以在两种盒子是否为空的情况（如情况一二和情况三四）之间直接通过加球、删球来进行转换。

对于球不同的情况，我们还需要一点前置知识。

3. 前置知识2

3.1 第二类斯特林数

第二类斯特林数的定义和球盒模型相似：把个不同的数划分为个集合的方案数，要求不能有空集。

设第二类斯特林数为。对于，可以通过以下两种情况来递推：

1、前个数划分为个集合，剩下第个数单独为一个集合，方案数为；

2、前个数划分为个集合，剩下第个数放到这个集合之中，方案数为。

因此递推式为。

递推是的。然而，关于第二类斯特林数，有单独的公式：.

时间复杂度瓶颈为快速幂的复杂度。

说来惭愧，作为一名ICPC银牌选手，我却从来没有了解过斯特林数。我记得不知道哪里的比赛考的裸的第二类斯特林数，当时我对着这个自己推出来的的递推式想了半天怎么优化，想了一个小时想不出来，只能眼睁睁看着一堆人把这题过了，然后怀疑人生。赛后才知道有斯特林数这个东西。

4. 正文1

5. 球不同，盒子相同，盒子不可以为空

这个问题与第二类斯特林数一致。直接根据公式求即可。

6. 球不同，盒子相同，盒子可以为空

一种显然的想法：枚举不空盒子的个数，将对应的答案累加即可。

答案为。

特殊地，若，那么问题等价于将大小为的集合进行划分的所有方案数。

7. 球不同，盒子不同，盒子可以为空

这个问题就非常简单了。对于每一个数，你都可以有个盒子选择，答案显然为。

8. 球不同，盒子不同，盒子不可以为空

由于球不同，所以没办法通过将每个盒子进行减球来将问题转化为上一个情况。

考虑和第二类斯特林数（第五个情况）之间的差异，可以发现控制变量为：盒子不同了。

也就是说每个盒子都有了标号。所以很简单，我们只需要将第二类斯特林数乘上全排列个数就可以了，答案为。